Chapter 3: Bijections and Combinatorial Proofs #

If one proves the equality of two numbers $a$ and $b$ by showing first that $a \leq b$ and then that $a \geq b,$ it is unfair; one should instead show that they are really equal by disclosing the inner ground for their equality.

— Emmy Noether

Hence, counting is sometimes just a pretext and the important thing is to understand, or discover, a structure in some discrete objects.

— Mireille Bousquet-Mélou

Our first general tool for the study of combinatorial classes is the notion of a bijection. Bijections allow us to use information about simple classes and classes we already understand to study complicated classes and classes we haven’t seen before.

Let $A$ and $B$ be two sets. We say that a function $f:A\rightarrow B$ is

injective if $a \neq a^\prime$ implies $f(a) \neq f(a^\prime)$ for any $a,a^\prime \in A,$
surjective if for every $b \in B$ there exists some $a \in A$ with $f(a)=b,$
bijective if it is injective and surjective.

If there is a bijection from $A$ to $B$ then we say that $A$ and $B$ are in bijection.

Remark: An equivalent formulation for injectiveness is that $f$ is injective if for all $a,a^\prime\in A$ the equality $f(a)=f(a^\prime)$ implies $a=a^\prime.$ This is the contrapositive to the statement above.

Because a bijection takes distinct elements of $A$ to distinct elements of $B,$ and every element of $B$ is mapped to by some element of $A,$ a bijection “pairs up” the elements of $A$ and $B$ (when $A$ and $B$ are infinite we usually define them to have the same size if and only if they are in bijection).

Exercise: Prove that if $A$ and $B$ are finite sets in bijection then $|A|=|B|.$

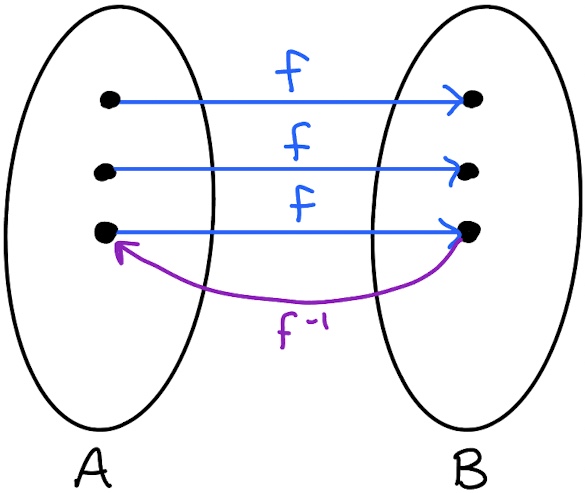
Figure: A bijection from $A$ to $B$ pairs up the elements of $A$ and $B.$

If $f:A \rightarrow B$ then we call a function $g:B\rightarrow A$ the inverse of $f$ if $$ g(f(a)) = a \text{ for all $a \in A$ \textbf{ and } } f(g(b)) = b \text{ for all $b \in B.$} $$ In other words, $g$ is the inverse of $f$ if applying the functions consecutively (in either order) to any element always gives back the starting element. We usually use the notation $f^{-1}$ for the inverse of $f$ when it exists.

Lemma 1: The function $f:A\rightarrow B$ is a bijection if and only if $f$ has an inverse.

Proof of Lemma 1

First, suppose that $f$ has an inverse $f^{-1}.$ Then $f$ is injective since applying the inverse to both sides of the equation $f(a)=f(a^\prime)$ implies $a=a^\prime,$ and $f$ is surjective since for any $b \in B$ the element $f^{-1}(b) \in A$ satisfies $f(f^{-1}(b))=b.$ Thus, when $f$ has an inverse then $f$ is a bijection.

Conversely, suppose that $f$ is a bijection. Then, since $f$ is surjective, for any $b \in B$ there exists some element $g(b) \in A$ such that $f(g(b)) = b.$ Since $f$ is injective the element $g(b)$ is unique, so the map $b \mapsto g(b)$ is a well-defined function. By construction $f(g(b)) = b$ for any $b \in B.$ Furthermore, for any $a \in A$ we have $f(g(f(a))) = f(a)$ by applying the definition of $g(b)$ with $b=f(a),$ so $f$ being injective implies $g(f(a))=a.$ We thus see that when $f$ is a bijection then it has an inverse.

The two most common ways of proving sets $A$ and $B$ are in bijection are thus

Define a map $f:A\rightarrow B$ and then prove
- that $f$ is well-defined (it actually takes elements of $A$ to elements of $B$)
- that $f$ is injective, and
- that $f$ is surjective.
Define two maps $f:A\rightarrow B$ and $g:B\rightarrow A,$ and prove
- that both maps are well-defined,
- that $g(f(a)) = a$ for all $a \in A,$ and
- that $f(g(b)) = b$ for all $b \in B.$

Example: Prove that the set of integers $\mathbb{Z}$ and the set of even integers $2\mathbb{Z} = \{\dots,-4,-2,0,2,4,\dots\}$ are in bijection.

Click for Answer

Define the functions $f:\mathbb{Z}\rightarrow2\mathbb{Z}$ and $g:2\mathbb{Z}\rightarrow\mathbb{Z}$ by $f(z)=2z$ and $g(z) = z/2.$ Note that $f$ and $g$ are well-defined since $f$ always outputs an even integer and $g$ always outputs an integer (because it only takes even integers as input). Then $g(f(a))=(2a)/2=a$ and $f(g(b))=2(b/2)=b$ for all $a\in\mathbb{Z}$ and $b\in2\mathbb{Z}$ so $g$ is the inverse function of $f$ and $f$ is a bijection.

Example: A permutation matrix of size $n$ is an $n\times n$ matrix with entries in $\{0,1\}$ where every row and every column has exactly one 1. Prove that the class $S$ of permutations and the class $M$ of permutation matrices are in bijection.

Click for Answer

Let $f:S \rightarrow M$ be the function that takes a permutation $\sigma = \sigma_1 \cdots \sigma_n$ of size $n$ and returns the $n \times n$ matrix with ones in positions $(1,\sigma_1),\dots,(n,\sigma_n).$

We prove that $f$ is a bijection by showing that

$f$ is well-defined,

$f$ is injective, and

$f$ is surjective.

We prove these properties in order.

If $\sigma$ is a permutation then $\{\sigma_1,\dots,\sigma_n\} = \{1,\dots,n\},$ so $f(\sigma)$ is an $n\times n$ matrix with one 1 in each row and each column.

If $f(\sigma)=f(\tau)$ then $\sigma$ and $\tau$ must be permutations of the same size $n$ and $\sigma_j = \tau_j$ for each $1 \leq j \leq n,$ so $\sigma = \tau.$

Let $L$ be a matrix in $M.$ If $L$ has ones in positions $(1,j_1),\dots,(n,j_n)$ then $\sigma = j_1 \; j_2 \; \cdots \; j_n$ is a permutation of size $n$ and $f(\sigma)=L.$

Thus, $f$ is a bijection between the combinatorial classes $S$ and $M.$

How do we find bijections? Bijective combinatorics can be more of an art than a science, however there are some useful tips to keep in mind.

Look at small examples. If you want to prove that two classes with objects $A$ and $B$ are in bijection then try to pair up the objects of size 1 in $A$ with the objects of size 1 in $B.$ Try to do the same thing for objects of sizes 2 and 3. Can you see a general pattern to pair up objects of any size $n$?
Think back to other bijections you’ve already seen. For instance, if you’re trying to find a bijection between a class of restricted permutations and a family of matrices, then can you reuse any ideas from our argument in the last example?
Try to decompose a complicated class into simpler parts. For instance, in a class whose objects are pairs then can you think about out where to send the first object in a pair and the second object in a pair independently?

A multiset of size $n$ with $t$ types is a sequence $(m_1,\dots,m_t) \in \mathbb{N}^t$ with $m_1 + \cdots + m_t = n.$

Exercise: Prove that the set of multisets of size $n$ with $t$ types is in bijection with the set of sets containing $n$ elements from $\{1,\dots,t\}$ where elements are allowed to repeat.

Lemma 2: If $n,t \in \mathbb{N}$ with $t \geq 1$ then there are $$ \binom{n+t-1}{t-1} $$ multisets of size $n$ with $t$ types.

Proof Sketch of Lemma 2 (‘Balls and Lines Bijection’)

Let $M$ be the set of solutions to $m_1 + \cdots + m_t = n$ with $(m_1,\dots,m_t) \in \mathbb{N}^t.$ The idea is to picture dividing $n$ balls into $t$ bins by drawing $t-1$ lines between $n$ balls to denote the boundaries between the $m_j.$

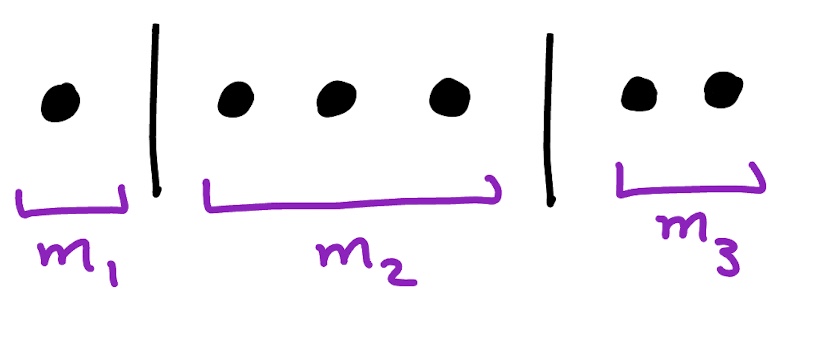
Figure: Representing the multiset $1 + 3 + 2$ of size 6 with 3 types by a sequence of 6 balls and 2 lines.

Formally, let $I$ be the tuples of length $n+t-1$ defined by $n$ identical balls and $t-1$ identical lines. Then $|I| = \frac{(n+t-1)!}{n!(t-1)!} = \binom{n+t-1}{t-1}$ since there are $(n+t-1)!$ ways to create such a tuple when all elements are distinct, dividing out by $n!$ accounts for the fact that all $n$ balls are identical, and dividing out by $(t-1)!$ accounts for the fact that the $t-1$ lines are identical.

Let $f:M \rightarrow I$ be the map that takes $(m_1,\dots,m_t) \in M$ and returns the tuple which, from left to right, contains $m_1$ balls followed by a line, then $m_2$ balls followed by a line, and so on until ending with $m_t$ balls. Lemma 2 follows from the following exercise.

Exercise: Prove that $f$ is a bijection.

Combinatorial Proofs #

Bijections and counting methods allow us to give combinatorial proofs of identities. To prove an identity of the form $$ \text{LHS} = \text{RHS} $$ there are two common approaches.

Find two sets $A$ and $B$ where it is easy to prove $|A| = \text{LHS}$ and $|B| = \text{RHS}$ and then prove that $A$ and $B$ are in bijection.
Count a single set $A$ in two different ways, one of which shows that $|A| = \text{LHS}$ and the other of which shows that $|A| = \text{RHS}.$

Combinatorial proofs stand in contrast to algebraic proofs, because they show equality by giving meaning to both sides of an equation instead of performing symbolic manipulations. We now give two simple examples to illustrate the method. Both of our examples are fairly easy to prove algebraically, but the method of combinatorial proof can be very powerful (especially once one has build up a large “dictionary” of combinatorial objects and their counting sequences).

Example: Give a combinatorial proof that $$ \binom{n}{k} = \binom{n}{n-k} $$ for any $n,k\in\mathbb{N}$ with $0 \leq k \leq n.$

Click for Answer

Let $A$ be the set of subsets of $[n]=\{1,\dots,n\}$ of size $k$ and $B$ be the set of subsets of $[n]$ of size $n-k,$ so that $|A| = \binom{n}{k}$ and $|B| = \binom{n}{n-k}.$

Consider the function $f:A\rightarrow B$ which takes an element $S \in A$ to its complement $f(S) = [n] \setminus S.$ Then $f$ takes a subset of $[n]$ with $k$ elements to a subset with $n-k$ elements, so it is well-defined. If $g:B \rightarrow A$ is also the complement function $g(T) = [n] \setminus T$ then $$g(f(S)) = [n] \setminus ([n] \setminus S) = S$$ for all $S \in A$ and, for the same reason, $f(g(T))=T$ for all $T \in B.$ Thus $g$ is the inverse of $f$ so $f$ is a bijection and $$ \binom{n}{k} = |A| = |B| = \binom{n}{n-k} .$$

Example: Give a combinatorial proof that $$ 2^n = \sum_{k=0}^n \binom{n}{k}. $$

Click for Answer

Let $A$ be the set of subsets of $[n]=\{1,\dots,n\},$ so $|A|=2^n.$ We can express $A$ as the disjoint union $$A = A_0 \cup \cdots \cup A_n$$ where $A_k$ denotes the subsets of $[n]$ with $k$ elements. Since $|A_k| = \binom{n}{k}$ we see that $$ 2^n = |A| = \sum_{k=0}^n |A_k| = \sum_{k=0}^n \binom{n}{k}. $$

The key to giving combinatorial proofs of identities is to identify combinatorial objects that are counted by the terms on each side. Here are some sequences that appear frequently in identities, and some of the combinatorial objects that are counted by them.

Sequence	Combinatorial Interpretation
$n!$	permutations of size $n$
$2^n$	binary strings of length $n,$ subsets of $[n],$ compositions of size $n+1$
$A^n$	strings of length $n$ on alphabet of size $A$
$\binom{n}{k}$	subsets of $[n]$ with $k$ elements
$\binom{a+b}{a}$	lattice paths from $(0,0)$ to $(a,b)$ using $(1,0)$ and $(0,1)$
$\binom{n+t-1}{t-1}$	multisets of size $n$ with $t$ types
$a \times b$	Cartesian product of sets with sizes $a$ and $b$
$a + b$	union of disjoint sets with sizes $a$ and $b$

The online encyclopedia of integer sequence is a key tool that allows users to look up the combinatorial objects counted by the initial terms of a sequence. If you have an unknown sequence, plug some of the terms into the oeis, find another objected counted by the sequence, and then try to find a bijection. (If you find one, then update the entry on the oeis with your new information!)

Additional Problems #

Problem 1. For any positive $n\geq 1$ give a bijection between the set of subsets of $\{1,2,…,n\}$ with an even number of elements and the set of subsets of $\{1,2,…,n\}$ with an odd number of elements. Conclude that there are $2^{n-1}$ subsets of $\{1,2,…,n\}$ with an even number of elements.

Problem 2. Let $n\in\mathbb{N}$ be a natural number.

(a) Give a bijection between the sets $$ \begin{aligned} \mathcal{S} &= \{ (A,B) : \text{$A,B \subset [n]$ are disjoint} \} \\[+2mm] \mathcal{T} &= \{ (P,Q) : \text{$P\subset Q \subset [n]$} \} \end{aligned} $$

(b) Give a bijection between the sets $$ \begin{aligned} \mathcal{S} &= \{ (A,B,C) : \text{$A,B,C \subset [n]$ are pairwise disjoint} \} \\[+2mm] \mathcal{T} &= \{ (P,Q,R) : \text{$P\subset Q \subset R \subset [n]$} \} \end{aligned} $$

(c) Generalize parts (a) and (b).

Problem 3. Give combinatorial proofs of the following identities (all quantities are integers). $$ {\small \begin{aligned} \binom{n}{k} &= \binom{n-1}{k-1} + \binom{n-1}{k} && (1 \leq k \leq n) \\[+5mm] k\binom{n}{k} &= n\binom{n-1}{k-1} && (1 \leq k \leq n) \\[+5mm] \binom{n}{k} &= \binom{n-2}{k} + 2\binom{n-2}{k-1} + \binom{n-2}{k-2} && (2 \leq k \leq n) \\[+5mm] \binom{n}{m}\binom{m}{k} &= \binom{n}{k}\binom{n-k}{m-k} && (0 \leq k \leq m \leq n) \\[+5mm] \binom{n}{k}\binom{n-k}{\ell} &= \binom{n}{k+\ell}\binom{k+\ell}{\ell} && (0 \leq k+\ell \leq n) \\[+5mm] n2^{n-1} &= \sum_{i=0}^n \binom{n}{i}i && (1 \leq n) \\[+5mm] n(n-1)2^{n-2} &= \sum_{i=0}^n \binom{n}{i}i(i-1) && (2 \leq n) \\[+5mm] \binom{2n}{n} &= \sum_{i=0}^n \binom{n}{i}^2 && (0 \leq n) \\[+5mm] \binom{n+1}{k+1} &= \sum_{i=k}^n \binom{i}{k} && (0 \leq n,k) \\[+5mm] \binom{n+k+1}{k} &= \sum_{i=0}^k \binom{n+i}{i} && (0 \leq n,k) \\[+5mm] \binom{n+t-1}{t-1} &= \sum_{k=1}^t \binom{t}{k}\binom{n-1}{k-1} && (0 \leq n,t) \\[+5mm] \binom{2n}{n} &= 2\sum_{i=0}^{n-1} \binom{n-1+i}{i} && (1 \leq n) \\[+5mm] 3^{n} &= \sum_{k=0}^n \binom{n}{k}2^k && (0 \leq n) \\[+5mm] 4^{n} &= \sum_{k=0}^n \binom{n}{k}3^{n-k} && (0 \leq n) \\[+5mm] 4^{n} &= \sum_{k=0}^n \binom{2k}{k}\binom{2n-2k}{n-k} && (0 \leq n) \\[+5mm] \binom{n}{k}^2 &= \sum_{i=0}^k \binom{n}{i}\binom{n-i}{k-i}\binom{n-k}{k-i} && (0 \leq k \leq n)\\[+5mm] \binom{p+q}{n} &= \sum_{k=0}^n \binom{p}{k}\binom{b}{n-k} && (0 \leq n)\\[+5mm] \binom{2a+b+1}{b} &= \sum_{i=0}^b \binom{a+i}{i}\binom{a+b-i}{b-i} && (0 \leq a,b) \\[+5mm] \binom{3n+1}{n} &= \sum_{i=0}^n \binom{n+i}{i}\binom{2n-i}{n-i} && (0 \leq n) \\[+5mm] \binom{4n+2}{2n+1} &= 2\sum_{i=0}^n \binom{n+i}{n}\binom{3n+1-i}{n} && (1 \leq n) \\[+5mm] \end{aligned} } $$

Problem 4. A Dyck path of size $n$ is a sequence of $n$ upsteps $(1,1)$ and $n$ downsteps $(1,-1)$ that start at the origin and never go below the $x$-axis. A return in a Dyck path is a maximal sequence of consecutive downsteps that ends on the $x$-axis.

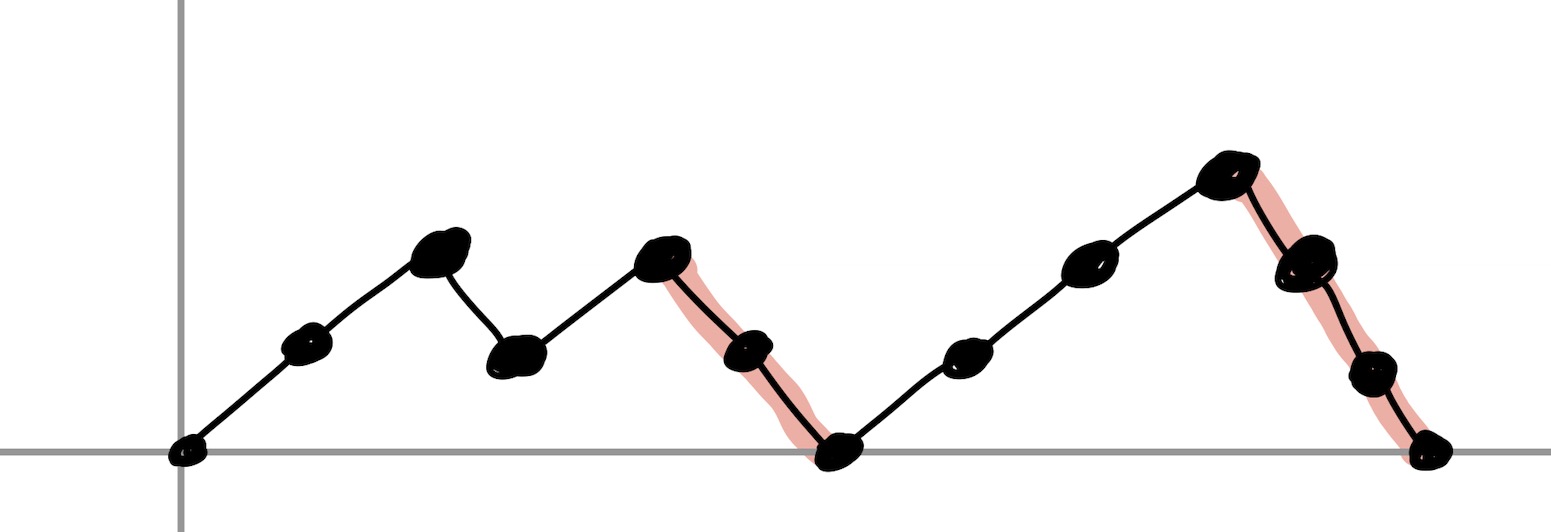
Figure: A Dyck path of size 6 that has returns of length two and length three (highlighted).

Prove that the set of Dyck paths of size $n-1$ is in bijection with the set of Dyck paths of size $n$ that have no returns with an even number of steps.

Problem 5. Fix a positive integer $k$ and define $$ \begin{aligned} \mathcal{S} &= \{(a_1, \dots, a_k) \in \mathbb{N}^k : a_j \text{ is divisible by } j \text{ for all j} \} \\[+2mm] \mathcal{T} &=\{(b_1, \dots, b_k) \in \mathbb{N}^k : b_1 \geq b_2 \geq \cdots \geq b_k \}. \end{aligned} $$ Give a bijection $f:\mathcal{S}\rightarrow\mathcal{T}$ such that $f((a_1, \dots, a_k)) = (b_1, \dots, b_k)$ implies $a_1 + \dots + a_k = b_1 + \dots + b_k$.