Chapter 14: Random Generation #

Random numbers should not be generated with a method chosen at random.

— Don Knuth

By a small sample we may judge of the whole piece.

— Miguel de Cervantes (Don Quixote de la Mancha)

Note: This chapter can be downloaded as a Sage Jupyter notebook from this link (or run in the browser at this link).

Instead of analytically determining asymptotics, another way to study the behaviour of combinatorial classes is to generate random objects of large size.

Uniform Random Generation #

A uniform generation algorithm for a combinatorial class $\mathcal{C}$ is a randomized algorithm that takes $n \in \mathbb{N}$ and returns an element in $\mathcal{C}$ of size $n,$ where every element of $\mathcal{C}_n$ is returned with probability $1/c_n.$

How do we generate randomness? Typically, we assume that we have access to a function rand() that returns a random real number in $[0,1).$

It is possible to construct rand using random coin flips (this is a topic for a computer science course). Whether there exists “true randomness” is also a question for computer science (or maybe philosophy).

We can use rand to generate a random integer in $\{0,\dots,n\}$ by defining $$\text{rand}(0\dots n) = \lfloor (n+1) \cdot \text{rand}() \rfloor$$

Our goal is to generate random algorithms that are correct, efficient, and easy to understand.

Below we discuss random generation using

Direct algorithms
Bijections
Recursive sampling
Boltzmann sampling (which is no longer uniform random generation)

Other common approaches to random generation include rejection sampling (randomly generate objects in a subset of the class you want until desired property holds) and ranking / unranking algorithms (efficiently order the elements in your class and then compute the $k$th element where $k$ random).

Direct Algorithms #

If the class is simple enough, we can directly implement a random generation algorithm.

Example: Find a uniform generation algorithm to compute a random binary string of length $n.$
Click for Answer
We directly generate binary digits one by one. In Sage code,
def rbin(n):
    # Every string appears with probability 1/2^n
    return [floor(2*RR.random_element(0,1)) for k in [1..n]]
where RR.random_element(0,1) returns a random real number in $(0,1).$ For instance, running rbin(10) returns (on the run saved in the Sage notebook corresponding to this chapter) [0, 1, 0, 1, 1, 0, 1, 0, 0, 0].

Bijections #

If we can randomly generate objects in a class $\mathcal{A},$ and know a bijection from $\mathcal{A}$ to another class $\mathcal{B},$ then we can randomly generate objects in the class $\mathcal{B}$ using the bijection.

Example: Find a uniform generation algorithm to compute a random subset of $\{1,\dots,n\}.$
Click for Answer
Recall we have a bijection $f$ from binary strings of length $n$ to subsets of $\{1,\dots,n\}$ where $f(b_1\cdots b_n) = \{k : b_k = 1\}.$ Thus, we can randomly generate subsets using the following code
def rset(n):
    b =  rbin(n)
    return [k+1 for k in range(n) if b[k]==1]
For instance, running rset(10) returns (on the run saved in the Sage notebook corresponding to this chapter) [1, 2, 4, 5, 8, 10].

Random Sampling #

How can we use combinatorial specifications to randomly generate elements?

As usual, we start with our base cases. In pseudocode,

def genϵ(n): 
    if n = 0 return ϵ
    else return NULL
    
def genZ(n): 
    if n = 1 return Z
    else return NULL

Combinatorial Sum #

Suppose $\mathcal{A} = \mathcal{B} + \mathcal{C}$ and we have uniform generation algorithms genB(n) and genC(n). How do we build genA(n)?

If $\alpha \in \mathcal{A}_n$ then $\mathbb{P}[\alpha \in \beta_n] = \frac{b_n}{a_n} = \frac{b_n}{b_n+c_n}$ so we define

def genBplusC(n):
    x = RR.random_element(0,1)
    if x < b(n)/(b(n) + c(n)) return genB(n)
    else return genC(n)

If $\alpha \in \mathcal{B}$ then it is returned with probability $$\frac{b_n}{b_n+c_n} \cdot \frac{1}{b_n} = \frac{1}{b_n+c_n} = \frac{1}{a_n},$$ and a similar argument works when $\alpha \in \mathcal{C},$ so we have a uniform random generation algorithm.

Combinatorial Product #

Suppose $\mathcal{A} = \mathcal{B} \times \mathcal{C}$ and we have uniform generation algorithms genB(n) and genC(n). How do we build genA(n)?

The probability that $\alpha \in \mathcal{A}_n$ is $\alpha = (\beta,\gamma)$ and $|\beta|=k$ is $\frac{b_kc_{n-k}}{a_n}.$ Thus, we first randomly generate the size that $\beta$ should have, then generate objects of the appropriate size from $\mathcal{B}$ and $\mathcal{C}.$

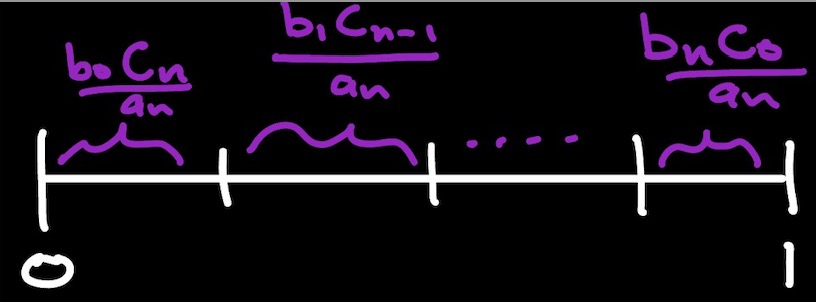
Figure: We can split the interval $[0,1]$ into *buckets* corresponding to the probabilities that a pair $(\beta,\gamma) \in \mathcal{B} \times \mathcal{C}$ of size $n$ has $|\beta|=k$ for $k=0,\dots,n.$

def genBtimesC(n): 
    x    = RR.random(0,1)
    k    = 0
    a(n) = sum(b(k)*c(n-k), k=0..n)
    s    = b(0)c(n)/a(n)
    while x>s:
        k = k + 1
        s = s + b(k)*c(n-k)/a(n)
    return [genB(k),genC(n-k)]

The probability that $(\beta,\gamma) \in \mathcal{B}_k \times \mathcal{C}_{n-k}$ is returned is $$ \frac{b_k \cdot c_{n-k}}{a_n} \cdot \frac{1}{b_k} \cdot \frac{1}{c_{n-k}} = \frac{1}{a_n},$$ so we have a uniform random generation algorithm.

Sequence #

If $\mathcal{B}$ has no objects of size $0$ then $A = \text{SEQ}(B)$ is equivalent to $$\mathcal{A} = \epsilon + \mathcal{B} \times \mathcal{A},$$ so the sequence construction can be captured by sum and product using a recursive algorithm.

Uniform Random Binary Trees #

Let’s combine the above discussion to create a uniform generation algorithm to for (unlabelled) binary rooted trees. Translating the specification $$\mathcal{B} = \epsilon + \mathcal{Z} \times \mathcal{B} \times \mathcal{B}$$ into Sage code gives the following.

# Recursive Generation Algorithm
# B = E + Z x B x B
def genTree(n):
    # Return ϵ from first part of +
    if n==0:
        return 'ϵ'

    Bn = binomial(2*n,n)/(n+1) # Counting sequence
    x = RR.random_element(0,1) # Random real in (0,1)

    # Find the size k of the first element in a pair of trees of size n-1
    k = 0
    s = (binomial(2*k,k)/(k+1) * binomial(2*(n-k-1),n-k-1)/(n-k))/Bn
    while x > s:
        k = k+1
        s = s + (binomial(2*k, k)/(k+1) * binomial(2*(n-k-1), n-k-1)/(n-k))/Bn
    
    # Return a tuple from the product
    return ['Z', genTree(k), genTree(n-k-1)]

For instance, running genTree(3) gives

Out: ['Z', ['Z', 'ϵ', 'ϵ'], ['Z', 'ϵ', 'ϵ']]

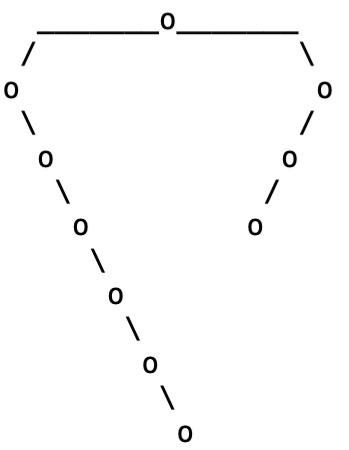
which corresponds to a binary tree whose root has two leaves for children.

Note: All outputs of our randomized algorithms are from the run saved in the Sage notebook corresponding to this chapter. It is highly recommend that readers run the code themselves to interactively play around with these algorithms!

In order to visualize our random binary trees, we rewrite the above code to use Sage’s built-in BinaryTree data structure.

# Change code to output 'BinaryTree' data structure
# which we use for plotting with Sage commands
def genTreePlot(n):
    # Return ϵ from first part of +
    if n==0:
        return None

    Bn = binomial(2*n,n)/(n+1) # Counting sequence
    x = RR.random_element(0,1) # Random real in (0,1)

    # Find the size k of the first element in a pair of trees of size n-1
    k = 0
    s = (binomial(2*k,k)/(k+1) * binomial(2*(n-k-1),n-k-1)/(n-k))/Bn
    while x > s:
        k = k+1
        s = s + (binomial(2*k, k)/(k+1) * binomial(2*(n-k-1), n-k-1)/(n-k))/Bn
    
    # Return a tuple from the product
    return BinaryTree([genTreePlot(k), genTreePlot(n-k-1)])

# Code to plot tree (with various plot options set)
def plotTree(BT):
    BT.graph().show(layout='tree',tree_orientation='down',figsize=(10,10),vertex_size=20, fig_tight=False, vertex_labels=False)

Running ascii_art(genTreePlot(10)) gives the following tree

A larger tree, with more advanced plotting, is obtained with the command plotTree(genTreePlot(100))

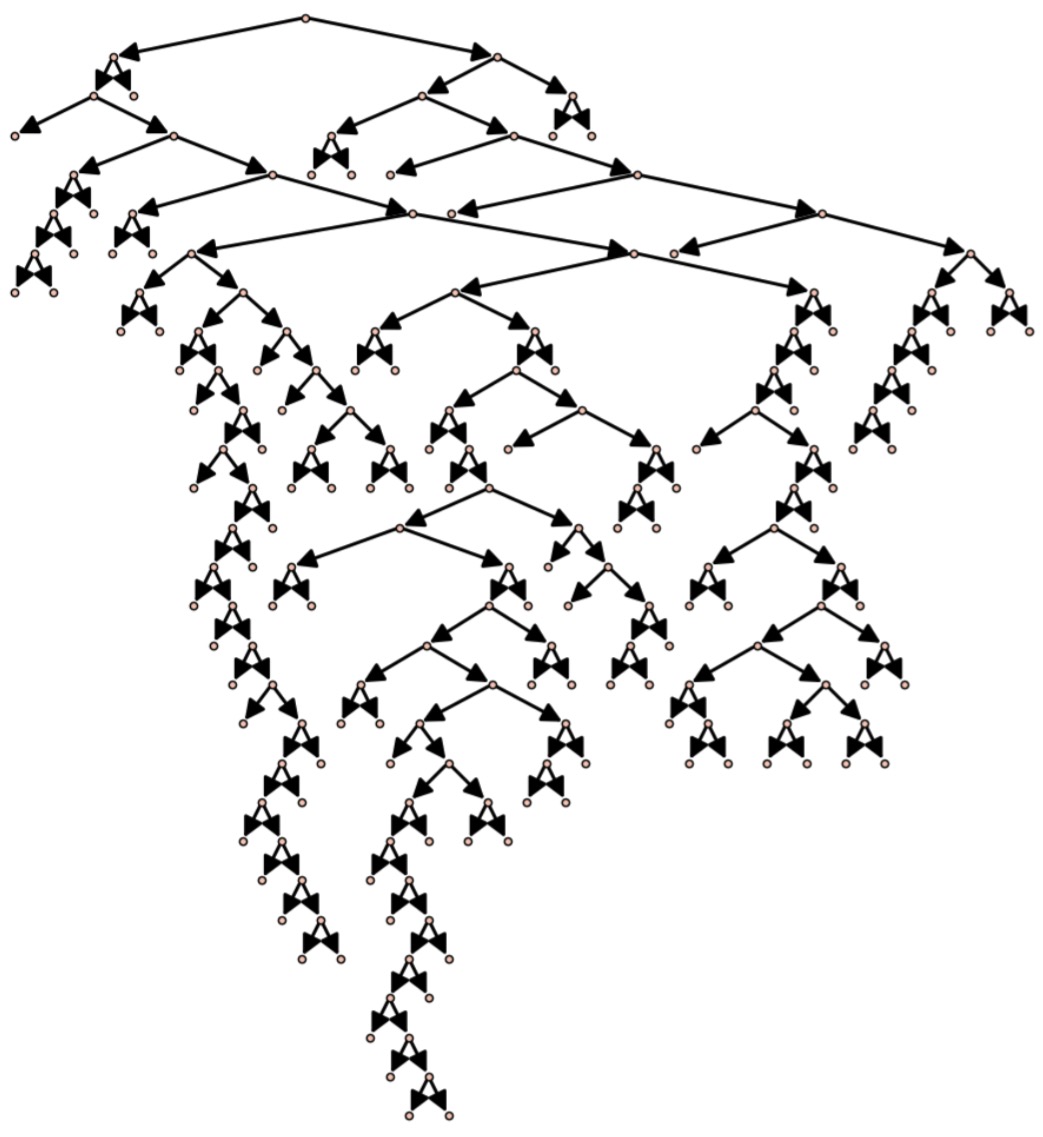
In addition to generating pretty pictures, we can also use this random generation algorithm to approximate statistics on binary trees.

For instance, recall that we previously used bivariate generating functions and LIFT to prove that the average number of leaves among the binary trees of size $n$ approaches $n/4$ as $n\rightarrow\infty.$ Running

from numpy import mean
N = 160
pt = [str(genTreePlot(N)).count('[., .]') for k in range(100)]
mean(pt)

returns the average number of leaves

Out: 40.7

among 100 randomly generated trees of size $160.$

In this manner, the automatic translation of specifications into random sampling algorithms gives a powerful tool for estimating the behaviour of combinatorial parameters (or a sanity check for analytically determined results). For instance, computing a histogram for the number of leaves in the trees computed above

plot(histogram(pt,bins=max(pt) - min(pt), density=True, range=[min(pt),max(pt)]))

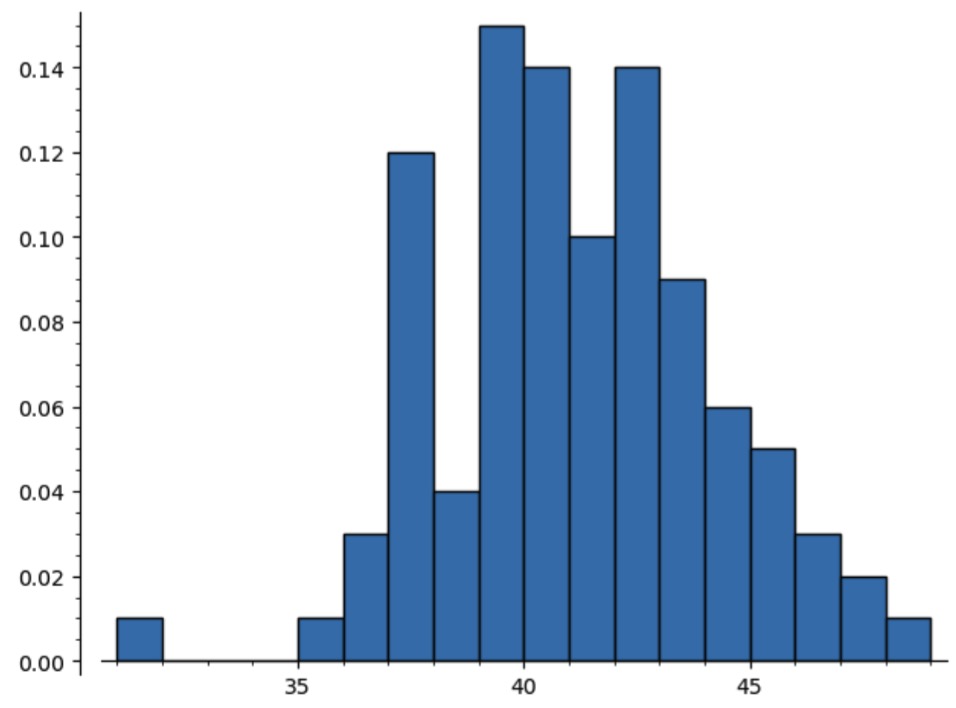
suggests that the number of leaves approaches a normal distribution (a result that can also be proven analytically, using more advanced methods).

Note: We develop general methods to compute random generation algorithms for a variety of combinatorial classes, but it is often possible to create more efficient methods for specific classes by analyzing their particular structure. For instance, there are many well-studied algorithms for generating random binary trees.

Boltzmann Sampling #

Recursive sampling is powerful, but can be slow for complicated objects. Instead of saying we need an object of size $n,$ we can look for an object of size (say) $[0.9n,1.1n]$ and (in general) do better. The elegant framework for handling this is Boltzmann sampling.

Recall that if $F(z) = \sum f_nz^n$ has radius of convergence $R$ then $F(p)$ converges to a complex number for $|p| < R.$ We call the points $v \in (0,R)$ the admissible values of $F.$

Let $\mathcal{A}$ be a combinatorial class and $v$ an admissible value for $A(x).$

A Boltzmann model at $v$ assigns each $\alpha \in \mathcal{A}$ the probability $$\mathbb{P}_v(\alpha) = \frac{v^{|\alpha|}}{A(v)}.$$

Note that $$ \sum_{\alpha \in \mathcal{A}} \mathbb{P}_v(\alpha) = \frac{\sum_{\alpha \in \mathcal{A}} v^{|\alpha|}}{A(v)} = \frac{A(v)}{A(v)}=1.$$ and $\mathbb{P}_v(\alpha)$ depends only on $|\alpha|.$ A Boltzmann generation algorithm with parameter $v$ is a randomized algorithm that returns $\alpha \in \mathcal{A}$ with probability $\mathbb{P}_v(\alpha).$

The value $v$ is a parameter: we can “tune” it to get objects of roughly the size we want. The expected size of the Boltzmann algorithm with parameter $v$ is $$ \sum_{\alpha \in \mathcal{A}} |\alpha| \mathbb{P}_v(\alpha) = \frac{\sum_{\alpha \in \mathcal{A}} |\alpha| v^{|\alpha|}}{A(v)} = \frac{vA^\prime(v)}{A(v)},$$ so we typically solve $n=\frac{vA^\prime(v)}{A(v)}$ for $v\in(0,R),$ if possible.

Example: For rooted binary trees with generating function $$B(z) = \frac{1-\sqrt{1-4z}}{2z}$$ we have seen in past chapters that $R = 1/4.$ The following table shows the probabilities of generating trees of size $n=0,1,2,3$ for different values of $v$ approaching $R.$ The expected sizes of the trees generated are approximately

$0.14$ if $v = 0.1$

$0.62$ if $v = 0.2$

$24.5$ if $v = 0.2499$

$v$ \ $n$	0	1	2	3
0.1	0.88	0.09	0.01	0.001
0.2	0.72	0.14	0.02	0.005
0.2499	0.51	0.13	0.03	0.01

Building Boltzmann Samplers #

The neutral class $\epsilon$ has generating function $1$ so its Boltzmann generator always returns a single $\epsilon$ with probability $v^0/1 = 1.$ The atomic class has generating function $z$ so its Boltzmann generator always returns a single atom with probability $v^1/v = 1.$

BOLT-ϵ(v): return ϵ
BOLT-Z(v): return Z

What about our constructions?

Combinatorial Sum #

Suppose $\mathcal{A} = \mathcal{B} + \mathcal{C}$ and we have Boltzmann generation algorithms BOLT-B(v) and BOLT-C(v). How do we build BOLT-A(v)?

The probability that $\alpha \in \mathcal{A}$ comes from $\mathcal{B}$ should be $$ \sum_{\beta \in \mathcal{B}} \frac{v^{|\beta|}}{A(v)} = \frac{B(v)}{A(v)} \in (0,1).$$

Note: Any admissible value for $A(z)$ is also admissible for $B(z).$

def BOLT-A(v):
    u = RR.random(0,1)
    if u < B(v)/A(v) return BOLT-B(v)
    else return BOLT-C(v)

Combinatorial Product #

Suppose $\mathcal{A} = \mathcal{B} \times \mathcal{C}$ and we have Boltzmann generation algorithms BOLT-B(v) and BOLT-C(v). How do we build BOLT-A(v)?

If $\alpha = (\beta,\gamma)$ then $$\frac{v^{|\alpha|}}{A(v)} = \frac{v^{|\beta| + |\gamma|}}{A(v)} = \frac{v^{|\beta|}}{A(v)} \cdot \frac{v^{|\gamma|}}{A(v)}.$$

This means each component is independent.

def BOLT-A(v):
    return [BOLT-B(v), BOLT-C(v)]

This is much easier than recursive sampling.

Sequence #

If $\mathcal{A}=\text{SEQ}(B)$ we can still use the recursive trick discussed above, but can also be more direct.

The probability that a specific tuple $(\beta_1,\dots,\beta_k)$ appears is $$\frac{v^{|\beta_1| + \cdots + |\beta_k|}}{1/(1-B(v))} = \frac{v^{|\beta_1|}}{B(v)} \cdots \frac{v^{|\beta_k|}}{B(v)} \cdot B(v)^k \cdot (1-B(v)),$$ so, the probability that a $k$-tuple appears should be $$\sum_{\beta_1,\dots,\beta_k \in \mathcal{B}} \frac{v^{|\beta_1|}}{B(v)} \cdots \frac{v^{|\beta_k|}}{B(v)} \cdot B(v)^k \cdot (1-B(v)) = B(v)^k (1-B(v)).$$

This is known as a geometric distribution.

def BOLT-A(v):
    k = Geometric(B(v))
    return k-tuple [BOLT-B(v),...,BOLT-B(v)]

We can sample from geometric distributions using a simple algorithm.

# Output natural number k with P(k returned) = λ^k*(1-λ)
def Geometric(λ):
    # Check if λ in (0,1)
    if not (λ > 0 and λ <1): 
        return "Error (λ must be in (0,1))"
    
    u = RR.random_element(0,1) # Random real in (0,1)
    k = 0
    s = 1 - λ
    while s < u:
        k = k+1
        s = s + λ^k*(1-λ)
    
    return k

Boltzmann Binary Trees #

Translating the specification $$\mathcal{B} = \epsilon + \mathcal{Z} \times \mathcal{B} \times \mathcal{B},$$ into a Sage Boltzmann sampler immediately gives the following.

def BoltzmannTree(x):
    u = RR.random_element(0,1)
    T = (1-sqrt(1-4*x))/(2*x)

    if u < 1/T: return 'ϵ' # Sum term
 
    return ['Z', BoltzmannTree(x), BoltzmannTree(x)] # Product term

Note how much simpler this is compared to the random sampling algorithm above. Running

[BoltzmannTree(0.2) for k in range(10)]

gives 10 randomly generated trees

[
 'ϵ',
 ['Z', ['Z', 'ϵ', 'ϵ'], 'ϵ'],
 ['Z', 'ϵ', 'ϵ'],
 ['Z', 'ϵ', 'ϵ'],
 ['Z',['Z', 'ϵ',['Z',['Z', 'ϵ', 'ϵ'],['Z',['Z', 'ϵ', 'ϵ'],['Z', 'ϵ',['Z', 'ϵ',['Z', 'ϵ',['Z', 'ϵ', 'ϵ']]]]]]],'ϵ'],
 'ϵ',
 'ϵ',
 ['Z', 'ϵ', 'ϵ'],
 'ϵ',
 'ϵ'
 ]

of which five have size 0, three have size 1, one has size 2, and one has size 10. Although the size of the tree returned is not fixed, recall that the output is always uniformly random with respect to all the binary trees of the same size as the output.

The fact that we see many trees of size 0 is not a coincidence. Indeed, randomly generating 1000 trees with parameter value $v=0.24$ relatively close to $R=0.25$ gives the probability histogram

xx = 0.24
pt = [str(BoltzmannTreePlot(xx)).count('[') for k in range(1000)]
pexp = plot(histogram(pt,bins=max(pt), density=True, range=[min(pt),max(pt)]))
pexp

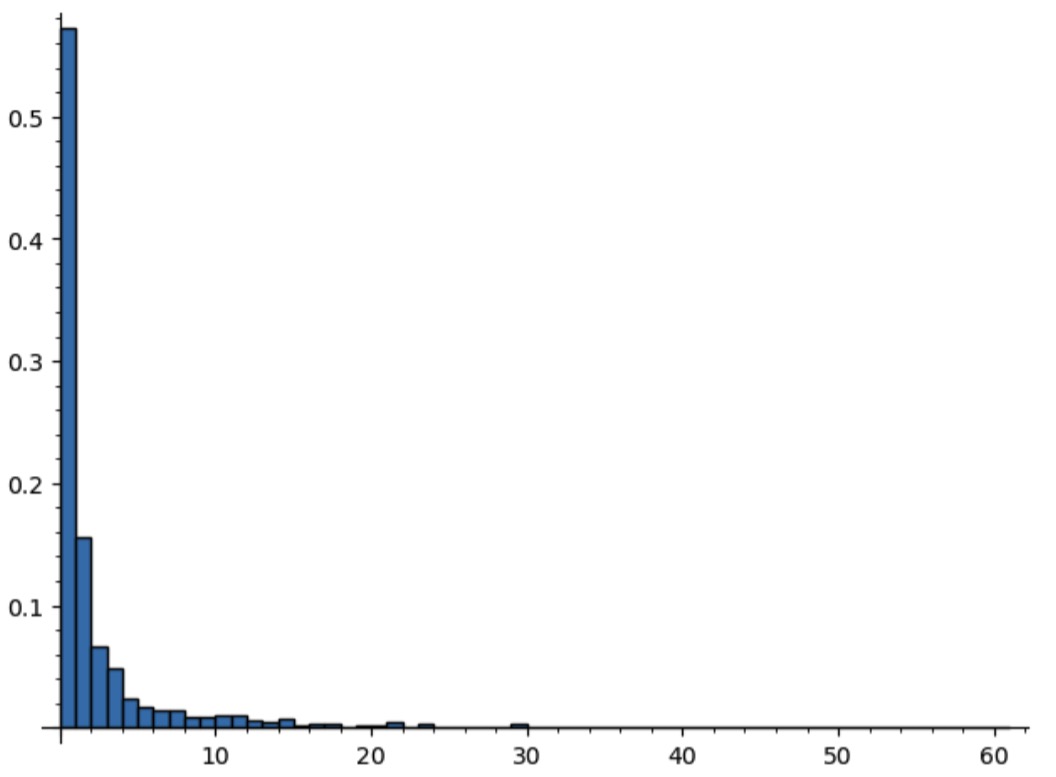
Thus, close to 60% of the generated trees will have size 0!

Boltzmann Theory and Marked Binary Trees #

The problem in our last example is that the distribution for the expected size of a generated binary tree, defined by $$ E(z) = \frac{zB^\prime(z)}{B(z)} $$ is too concentrated: the expected size $E(v)$ goes to infinity as $v\rightarrow 0.25,$ but only because there is a very small chance of generating a massive tree.

The theory of Boltzmann sampling was worked out in a wonderful paper of Duchon, Flajolet, Louchard, and Schaffer, from which we have adapted much of our presentation. In particular, under some natural assumptions we can repeatedly call a Boltzmann sampling algorithm until we get close to a desired size (within any constant fraction) and this approach has linear complexity in the desired size.

Theorem (Duchon-Flajolet-Louchard-Schaffer 2004): Fix $\epsilon>0$ and let $\mathcal{C}$ be a combinatorial class such that $C(z)$ has a finite radius of convergence $R>0,$ $$\lim_{z\rightarrow R^-} \frac{zC^\prime(z)}{C(z)} = \infty,$$ and a technical “variance condition” holds.

Let $z_n$ be the smallest positive root of $n = \frac{zC^\prime(z)}{C(z)}$ and repeatedly call BOLT-C(z_n) until it returns something with size in $[(1-\epsilon)n,(1+\epsilon)n].$ This happens with probability going to $1$ as $n\rightarrow\infty$ and on average takes $O(n)$ total operations.

Remark: Random generation has lots of practical applications (for instance, bugs in the Glasgow Haskell Compiler have been found by randomly generating large “λ-terms”).

To improve Boltzmann sampling for a specific class, we can consider related classes with less peaked distributions.

For instance, a marked rooted binary tree is a binary tree where one node is “marked”. Since all trees of size $n$ are marked in $n$ ways, we can randomly generate a rooted binary tree by generating a marked tree and forgetting which node is marked. Marking is useful for randomly generating object of large size, because objects of larger size can be marked in more ways.

If $\mathcal{B}^*$ is the class of marked rooted binary trees then $$ \mathcal{B}^* = \underbrace{\mathcal{Z}^* \times \mathcal{B} \times \mathcal{B}}_\text{root marked} \;+\; \underbrace{\mathcal{Z} \times \mathcal{B}^* \times \mathcal{B}}_\text{marker in left subtree} \;+\; \underbrace{\mathcal{Z} \times \mathcal{B} \times \mathcal{B}^*}_\text{marker in right subtree} $$ where, as usual, $\mathcal{B} = \epsilon + \mathcal{Z} \times \mathcal{B} \times \mathcal{B}.$

This leads to the following Boltzmann sampling algorithm (written using the Sage BinaryTree data structure for plotting).

def BoltzmannPointedTreePlot(x):
    var('z')
    u = RR.random_element(0,1)
    
    T = (1-sqrt(1-4*z))/(2*z)
    pointedT = z*T.diff(z)
    T = T.subs(z=x)
    pointedT = pointedT.subs(z=x)
    
    # handle union
    if u < x*T^2/pointedT:
        return BinaryTree([BoltzmannTreePlot(x), BoltzmannTreePlot(x)])
    if u < x*T^2/pointedT + x*pointedT*T/pointedT:
        return BinaryTree([BoltzmannPointedTreePlot(x), BoltzmannTreePlot(x)])
    
    return BinaryTree([BoltzmannTreePlot(x), BoltzmannPointedTreePlot(x)])

Now we have a size distribution that is much less bunched around the origin.

xx = 0.24
pt = [str(BoltzmannPointedTreePlot(xx)).count('[') for k in range(1000)]
plot(histogram(pt,bins=max(pt), density=True, range=[min(pt),max(pt)]))

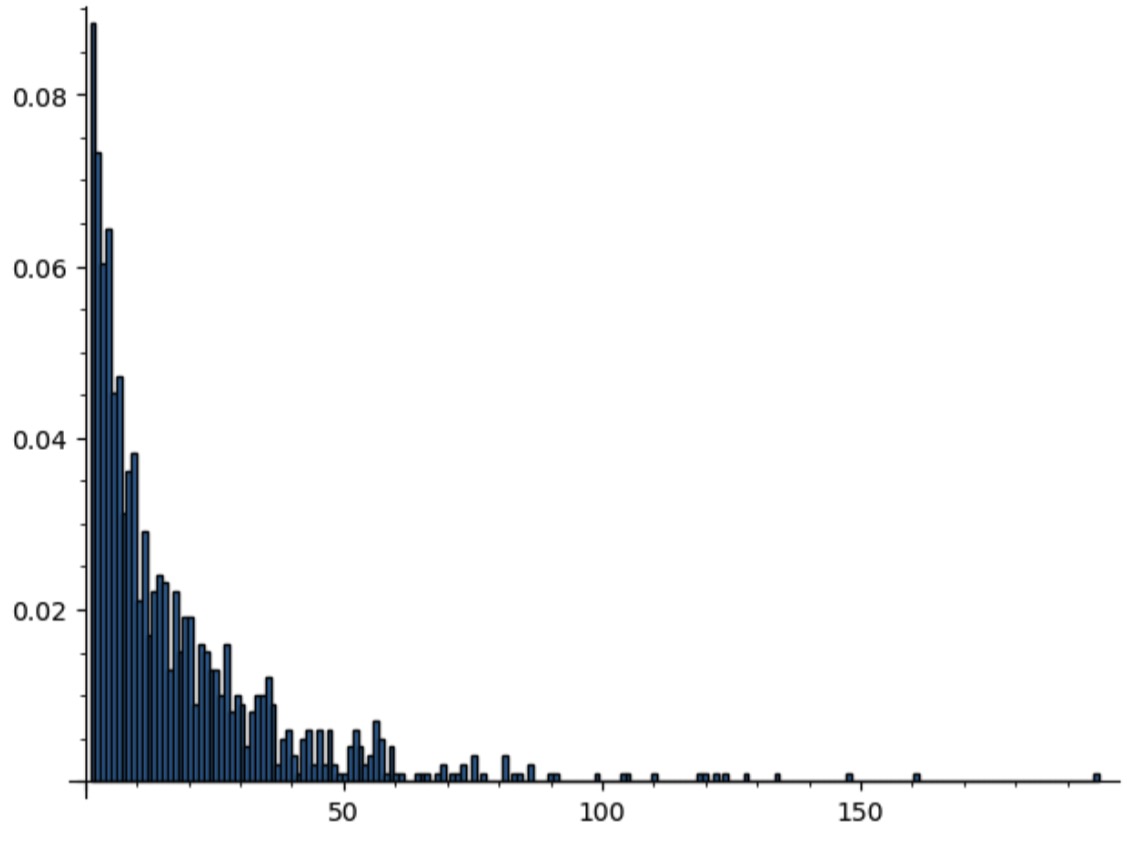
The following Boltzmann sampler repeats until it is within 10% of the input size.

# Helper function
def treeSize(BT): return str(BT).count('[')

# Repeatedly call Boltzmann sampler until tree of right size found
def BoltzmannReject(n):
    T = (1-sqrt(1-4*z))/(2*z)
    pointedT = z*T.diff(z)
    eq = (z*pointedT.diff(z)/pointedT) == n
    xx = eq.find_root(0,1/4)
    BT = BoltzmannPointedTreePlot(xx)
    while treeSize(BT)<0.9*n or treeSize(BT)>1.1*n:
        BT = BoltzmannPointedTreePlot(xx)
    return BT

For instance, running

plotTree(BoltzmannReject(300))

returns the following tree of size 311 in around 250 milliseconds

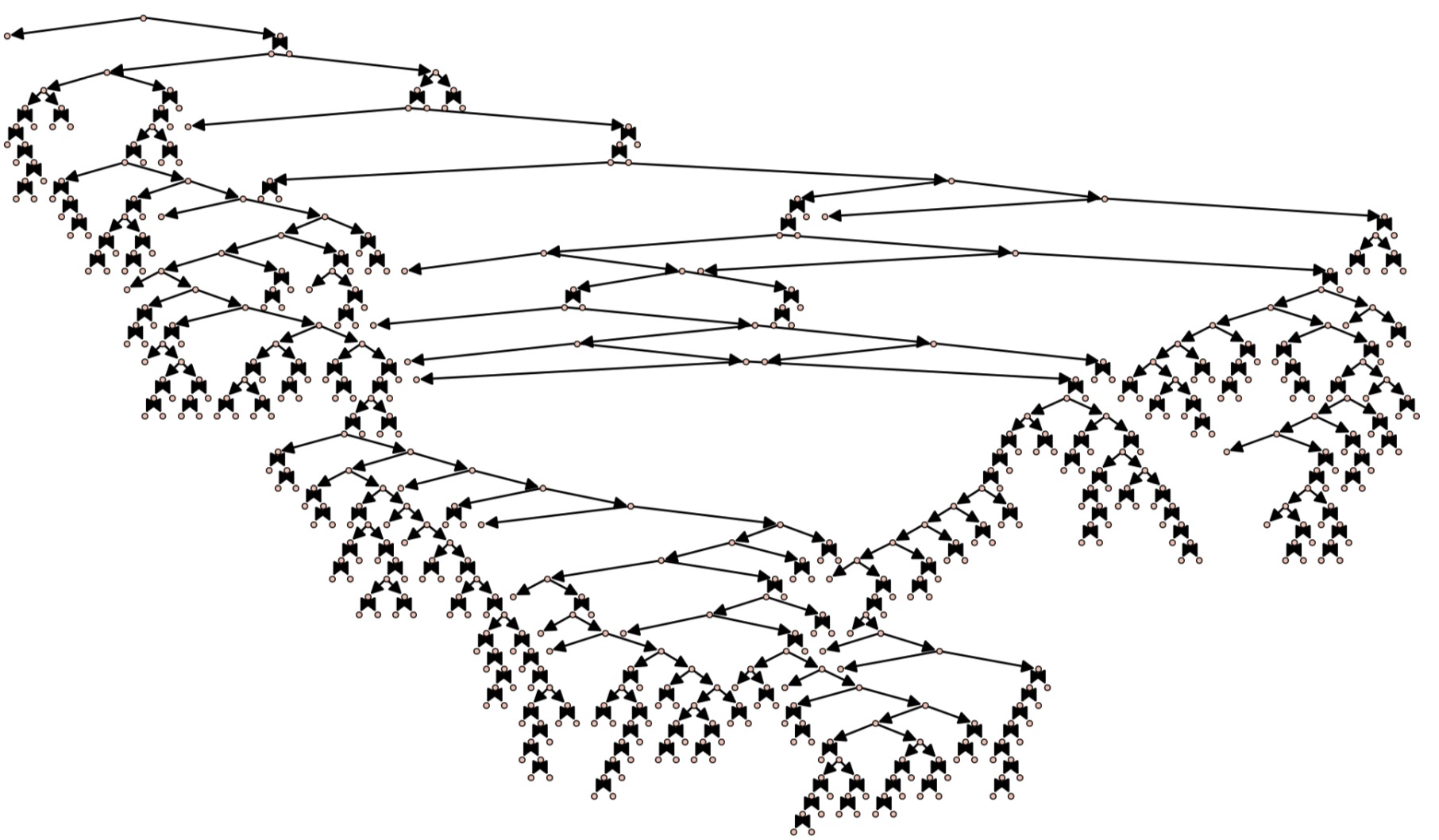
We also note that our (marked) Boltzmann sampling algorithm is more efficient than uniform random sampling. For instance, running

timeit('BoltzmannReject(1000)')
timeit('genTreePlot(1000)')

shows that Boltzmann sampling takes approximately 765 milliseconds to generate a tree of size within 10% of 1000, while recursive sampling takes approximately 2 seconds. This difference grows as the size of the trees gets larger.